Lecture 9: Breadth-First Search

Rrepresentations of Graph

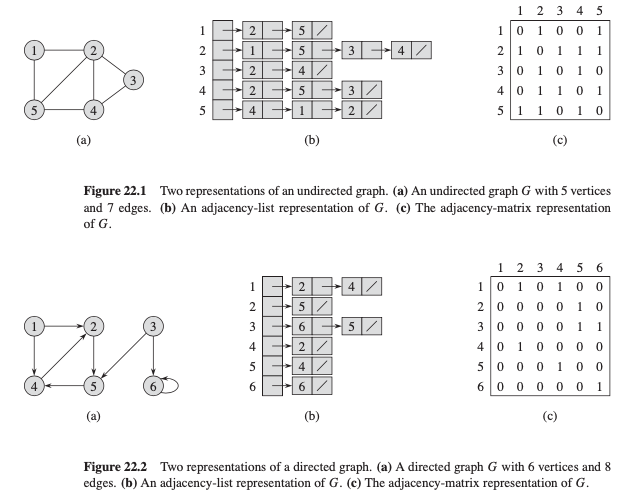
There are two ways to represent a graph \(G = (V, E)\): as a collection of adjacency lists or an adjacency matrix. Either way applies to both directed and undirected graphs.

• Adjacnecy-list representation provides a compact way to represent Sparse graphs: \(|E|\) is way less than \(|V^2|\).

• Adjacency-matrix representation when the graph is dense

  • can help quickly to tell if there is an edge connecting two vertices.

.

Adjancency-list Representation

• The graph \(G=(V,E)\) consist of an array G.Adj of \(|V|\) lists, one for each \(V\).

• For each \(u \in V\), the adjacency list \(Adj[u]\) containts all the vertices \(v\) such that there is an edge \((u,v) \in E\), or contains pointers to these vertices.

• The sum of length of all the adjacency lists

  • \(2*|E|\) for undirected graph

  • \(|E|\) for directed graph

• Similarly, we can define an associated attirbute \(w\) as \(G.w\) to represent weighted graphs. -. \(G.w[u]\).

• Disadvantages:

  • \(O(|E|)\) time to determine if an edge \((u, v)\) is present in the graph

Adjancency-matrix Representation

• The adjacency matrix \(A\) is \(|V|\)-by-\(|V|\) so that \(a_{i,j} = 1\) if \((i, j)\in E\) else 0

• Requires \(O(V^2)\) space

• Preferred when graphs are reasonably small.

Implementation of Vertex/Edge Attributes

• Attributes such as adjacency list, weights can be annotated as G.Adj, G.w.

• Similar for vertice or edge attributes: u.d, (u,v).f etc.

• But how to implement these attributes in programs??

  • depends on language and algorthm needs

Breadth-First Search

• Given a graph \(G\) and a distinguished source \(s\), BFS explores the edge of \(G\) to discover every vertex that is reachable from s and return a breadth-first tree with root s that contains the shortest path from s to v for each v reachable from s.

• breadth-first: discover all vertices at distance k from s before discovering any vertices at distance k+1.

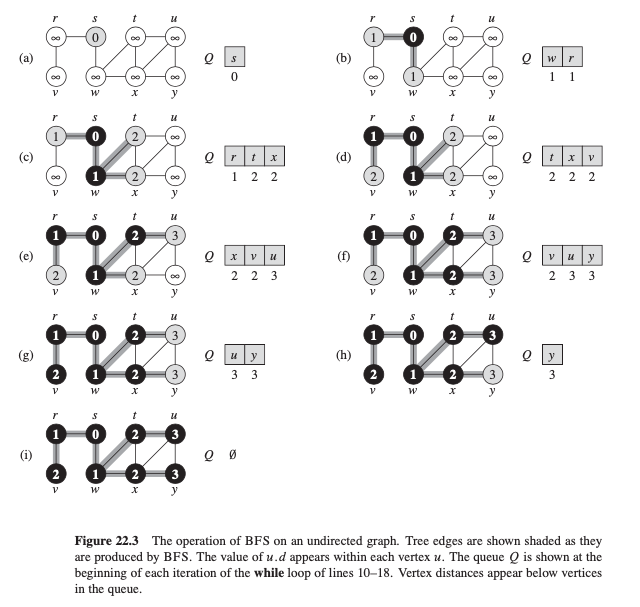
• psedocode: assuming adjacency-list representation

def BFS(G,s):
    for u in G.V:                       # Initialize all vertices --> O(V)
        u.color = WHITE                 # Mark all vertices as unexplored --> O(1)
        u.d = inifinity                 # Initialize the distance to infinity --> O(1)
        u.p = NIL                       # Initialize the parent to NIL --> O(1)
    s.color = GRAY                      # Start to explore vertice s --> O(1)
    s.d = 0                             # Set the root distance as 0 --> O(1)

    Q = []                              # Initialze a queue to store Gray vertices --> O(1)
    enqueue(Q, s)                       # Put root s in the queue --> O(1)
    while Q != []:                      
        u = dequeue(Q)                  # Dequeue Q to explore the first vertice u in the queue --> O(1)
        for v in G.Adj[u]:              # Explore adjacenct list of u --> O(E)
            if v.color == WHITE:        # If v is unexplored yet, add to the queue for exploring
                v.d = u.d + 1           # Update distance of v
                v.color == GRAY         # Mark vertice as exploring
                v.p = u                 # Set parent vertice
                queue(Q, v)             # Add vertice to queue for future exploring
        u.color = BLACK                 # Finish exploration of u and mark

Shortest Path

• After running BFS on a graph, we can get all the shortest paths from s to any reachable vertice v as a breadth-first tree

• How to obtain the shortest path from s to v??

  • run BFS on G

  • recursively check the parent of v until reach s

def shortest_path(G,s,v):
    if v==s:
        return s
    elif v.p == NIL
        print("No path from s to v exists")
    else:
        shortest_path(G, s, v.p)