Lecture 13: The Dijkstra’s Algorithm

Overview

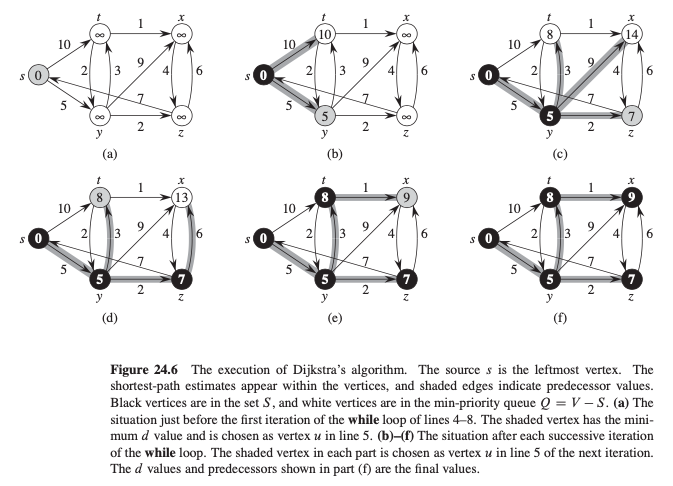
• Dijkstra’s algorithm solves the single-source shortest-paths problem on a weighted, directed graph G D .V; E/ for the case in which all edge weights are nonnegative

Dijkstra Algorithm

• Dijkstra’s algorithm maintain a set S of vetices whose final shortest-path weights from the source s have already been determined.

• The algorithm repeatedly

  • selects the vertex u in V-S with the minimum shortest-path estimate

  • adds u to S

  • relaxes all edges leaving u

• The implememtation relies on min-priority queue Q of vertices, keyed by their d values.

• The algorithm always chooses the “closest” vertex in V-S to add to set S, and therefore uses a greedy strategy. -> not always yield optimal results but can do the work.

   def Dijkstra(G, s):
1        initialize_single_source(G,s)
2        S = None                           # Initialize S
3        Q = G.V                            # Initialize min-priority queue Q
4        while Q not None:                  # 
5           u = delete_min(Q)               # Dequeue from min-priority Q
6           S += u                          # Insert to S
7           for v in G.Adj[u]:              # Relax adjacent vertice
8               relax(u, v, w)

• Example