Lecture 10: Depth-First Search

Overview

• search deeper wherever possible

• solve single source reacheability, not shortest path problem. Will be useful for solving other problems (later at XXX).

• return parent tree or forest (e.g., multiple trees)

DFS

• could run from a single source or multiple source

• As in breadth-first search, depth-first search colors vertices during the search to indicate their state. Each vertex is initially white, is grayed when it is discovered in the search, and is blackened when it is finished, that is, when its adjacency list has been examined completely. This technique guarantees that each vertex ends up in exactly one depth-first tree, so that these trees are disjoint.

• Besides creating a depth-first forest, depth-first search also timestamps each vertex.

  • Each vertex v has two timestamps: the first timestamp v.d records when v is first discovered (and grayed), and the second timestamp v.f records when the search finishes examining v’s adjacency list (and blackens v).

  • The timestamps provide important information about the structure of the graph and are generally helpful in reasoning about the behavior of DFS

  • The timestamps are integers between 1 and 2|V|.

  • For each v, \(v.d < v.f\).

• algorithm: DFS(G,s)

  • initialize global time stamp

  • mark the source vertice as gray, being explored

  • for vertex v in the adjacency list of s, if not explored yet, run DFS(G,v) recursively

  • mark source verice as black, finishing exploration

  • update time stamp by 1

  • assign final timestamp for source vertex

• examples

def DFS_source(G,s):                # An implementation of DFS for a single source
    for u in G.V:                   # Initialize search algorithm
        u.color = WHITE
        u.p = NIL

    global time = 0                 # Global time stamp. This should be set on the top level if DFS(G) calls DFS_single(G.s) to traverse all the vertice in G
    s.color = GRAY                  
    s.p = NIL                       
    s.d = time
    for v in G.Adj[s]:             # Recursively explore unexplored adajacent vertex
        if v.color == WHITE:
            v.p = s
            DFS(G,v)
    s.color = BLACK                # Mark as done for exploration
    time = time + 1                 
    s.f = time                     # Record final time for vertex

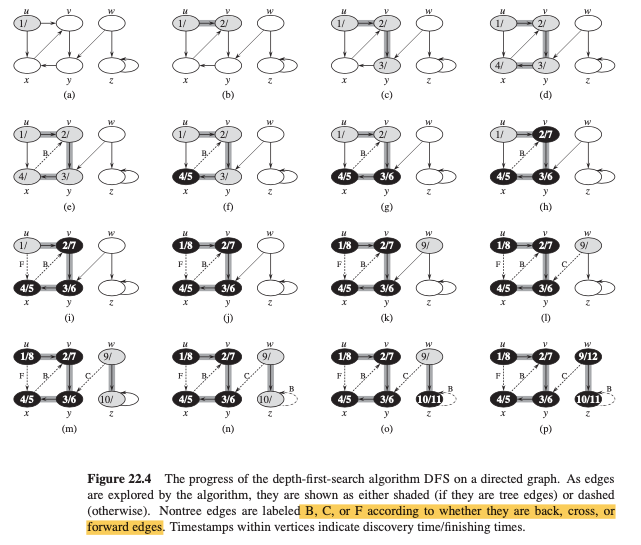
• DFS Tree Edges:

  • Type:

    • tree edges: edge (u, v) that v was first discovered by exploring edge (u,v).

    • back edges: edges (u,v) that connect with a vertex u to an ancestor v in a depth-first tree

    • forward edges: edges (u,v) that connect with a vertex u to an descendant v in a depth-first tree

    • cross edeges: They can go between vertices in the same depth-first tree, as long as one vertex is not an ancestor of the other, or they can go between vertices in different depth-first trees.

  • Colors:

    • WHITE: indicate a tree edge

    • GRAY: indicates a back edge

    • BLACK: indicates a foward or cross edge

  • In a depth-first search of an undirected graph G, every edge of G is either a tree edge or a back edge.

Topological Sort

• A topological sort of a directed acyclic graph \(G = (V, E)\) is a linear ordering of all its vertices such that if G contains an edge (u, v) then u appears before v in the ordering.

• If the graph contains a cycle, then no linear ordering is possible.

• We can view a topological sort of a graph as an ordering of its vertices along a horizontal line so that all directed edges go from left to right.

  def topological_sort(G):
      call DFS(G) to compute finishing time v.f for each vertex v
      as each vertex is finished, insert it onto the front of a linked list
      return the linked list of vertices