Lecture 12: The Bellman-Ford Algorithm

Overview

• The Bellman-Ford algorithm solves the single-source shortest-paths problem in the general case in which edge weights may be negative.

• The Bellman-Ford algorithm returns a boolean value indicating whether or not there is a negative-weight cycle that is reachable from the source.

  • If there is such a cycle, the algorithm indicates that no solution exists.

  • If there is no such cycle, the algorithm produces the shortest paths and their weights.

Bellman-Ford Algorithm

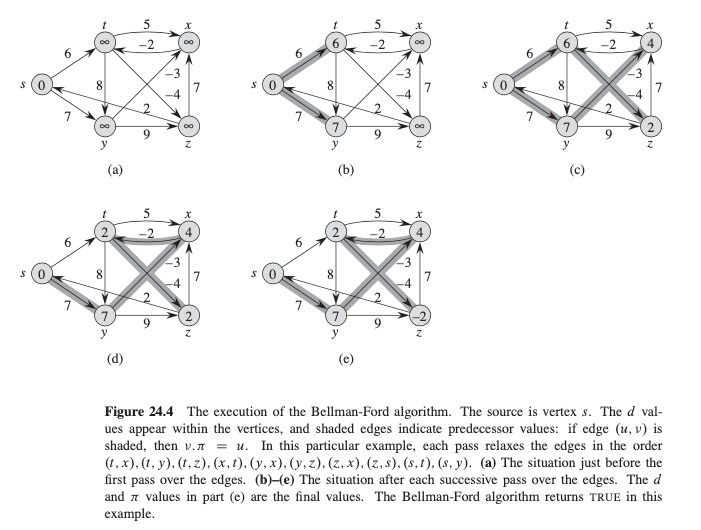
• Find the shortest paths from source \(s\) to every vertex \(v\) in a weighted graph. The weights may be negative

• Algorithm: \(O(VE)\)

   def bellman_ford(G, s):
       initialize_single_source(G,s)
       for i in range(len(G.V)-1):
           for (u,v) in G.E:
               relax(u,v,w)
       for (u,v) in G.E:
           if v.d > u.d + w(u,v):
               return False
       return True

• Example